Comme tout pédagogue a pu le constater dans sa vie quotidienne, sans pour autant l'avouer de peur qu'on le traite d'incompétent, la plupart des séances d'apprentissage portant sur des concepts fondamentaux donnent peu de résultats et les savoir-faire que l'élève parvient parfois à reproduire ne sont presque jamais réinvestis de façon pertinente dans d'autres temps de vie pour peu qu'ils ne soient pas un clone du premier. On pourrait donc être tenté de considérer ces séances comme des échecs. Pour ma part, je considère que l'on nomme communément concept le phénomène d'abstraction par lequel l'apprenant devient capable, à une juxtaposition de situations vécues, d'ajouter de son propre chef de nouvelles situations vécues ou pensées et de justifier son action de regroupement en évoquant d'une manière ou d'une autre le concept qui a justifié pour l'enseignement la mise en place de la première juxtaposition de vécus. Dés lors, il devient capable, de par cette abstraction, de créer des procédures propres aux situations nouvelles qui sous-tendent le concept en question, mais aussi de juger de manière pertinente d'autres procédures sans pour autant passer par leur mise à l'épreuve expérimentale. Cette approche conceptualisée des situations ne saurait se construire par une simple reproduction de procédures, fussent-elles explicitées, "métacognitionnées", et j'en passe. Elle passe obligatoirement par l'accumulation de situations vécues (situations problèmes, projets, jeux de rôle) dont le concept-objectif est sous-jacent, mais aussi par la capacité de l'élève à créer du liant entre ces situations en apparence différentes. Il faut bien avoir à l'esprit que cet élève, qui n'a pas encore construit le concept souhaité, ne peut que très difficilement établir ce "liant" par lui-même. Le rôle de l'enseignant est donc double : il doit à la fois organiser des temps de vie différents du point de vue sensible mais porteurs d'un même concept, mais aussi aider l'élève à façonner ce liant, c'est à dire organiser la juxtaposition mentale de ces temps de vie. Dans cette optique, la seule organisation efficace des traces écrites* serait la mise en place de classeurs d'occurrences conceptuelles où à chaque intercalaire correspondrait un concept, où on laisserait une très courte évocation de la situation présente chaque fois qu'un concept est mis en jeu. Au cycle 3 notamment, une même situation, surtout dans le cadre d'un projet, peut amener des traces dans plusieurs concepts, parfois dans des matières différentes. Le caractère bref de ces rappels fait appel à la mémoire de l'élève, donc l'enseignant doit veiller à ce que les temps de vie liés aux occurrences conceptuelles soient des temps forts d'un point de vue affectif, d'où le recours aux jeux, aux projets, aux TICE et à diverses formes d'humour. Bien sûr, la construction effective et efficace des concepts clés de l'enseignement primaire s'étale généralement sur plusieurs années et les vacances d'été ne doivent pas effacer les juxtapositions de vécus en cours d'enrichissement. Un classeur d'occurrences conceptuelles doit donc être conservé et poursuivi tout au long de la construction des concepts qu'il contient et pour tous les élèves du groupe de travail, c'est à dire du CP au CM2, voire jusqu'au collège. La géométrie est la matière par excellence où les concepts abstraits foisonnent. Il est donc fondamental de l'aborder en ayant à l'esprit toutes ces réalités didactiques. Nous allons voir comment, dans une classe de CE1, l'enseignement de la géométrie peut et doit renvoyer à des situations disparates par leur sensibilité, et qui pourtant posent les points d'ancrage de juxtapositions conceptuelles qui prendront au moins 2 ou 3 ans avant d'enfanter d'une première forme d'abstraction géométrique.
* La trace écrite peut aussi être conçue en terme d'outils, mais dés lors, il faut admettre qu'une affiche bien placée et établie en partenariat avec les élèves est plus utile qu'un cahier qu'il faut retrouver et ouvrir à la bonne page le cas échéant.
Le plan est un univers en 2 dimensions qui s'étend dans toutes les directions jusqu'à l'infini, c'est à dire sans jamais s'arrêter. Avec les enfants, il vaut mieux dire "ne s'arrête jamais" que "jusqu'à l'infini" car ils ont tendance à considérer l'infini comme le dernier nombre fini. Avec mes CE1, j'ai introduit ce plan avec une simple feuille de papier déchirée. La déchirure est ce qui symbolise par connivence la continuité le l'objet de pensée au-delà de l'objet réel. Bien sûr, cela ne prendra sens que plus tard pour l'élève. A cette première acception du plan, qui amène par pliage à la droite et au secteur angulaire (potentiellement "droit"), il convient d'ajouter rapidement celle du plan comme espace de travail. C'est alors la multiplication des occurrences matérielles disparates de ce que l'on considère comme plan qui va permettre l'abstraction et l'idée de "grandeur" du plan. Le plan (de travail !), ce sera à la fois la feuille de papier (A4, A3, etc...), le tableau, le panneau d'affichage cartonné, un mur, le sol de la cour de récréation, une plage à marée basse (à proximité ou à l'occasion d'une classe de mer), le terrain de football dont les lignes sont bonnes à refaire, mais aussi l'écran d'ordinateur dans le cadre de l'utilisation d'un logiciel de géométrie dynamique. Cette multiplicité des supports ne permet pas de faire l'économie d'une vraie d'explicitation sur la langue française (plan = plat). Cette explicitation langagière nous amènera à exclure les surfaces que l'on ne peut pas considérer comme de vrais plans (ballon, taule ondulée, parapluie, bouteille, corps humain). En fin d'apprentissage, un débat sur le cas de la Terre, et sur les conséquences des conclusions qui pourraient voir le jour (!), permettra d'introduire ou d'approfondir la dualité constamment ambiguë du monde conceptuel et du monde réel. Mais là, nous ne sommes déjà plus en CE1...
La droite s'obtient par le pliage d'un plan. Elle sépare le plan en 2 moitiés superposables, et donc à cette fin, ne s'arrête jamais non plus. Introduite de façon scientifique par le pliage du plan précédent, elle se matérialise par des objets nommés "règles" et dont la première occurrence est cette vulgaire feuille de papier pliée, au trois quart déchirée. La notion de droite va être construite d'une part par la multiplication des règles différentes : règle de papier de taille variable, règle de plastique, règle en bois d'un mètre au tableau, corde tendue dans la cour, boîte en carton ; et d'autre part au travers de la recherche d'autres occurrences matérielles, que l'on confronte à la redoutable corde tendue, et que l'on peut le cas échéant considérer comme relevant de la même "idée" quand bien même leur utilisation matérielle en tant que règles serait périlleuse. Il y a aussi bien sûr la représentation des logiciels de géométrie dynamique. L'ensemble des figures dont la représentation acceptable nécessite une règle représente à chaque fois de nouvelles occurrences de ce concept, même si on parle aussi de segments. Enfin, on devra veiller à ce que tout trait ne soit pas considéré comme une droite et on exclura par exemple le rond, l'ovale, la patate, et bien sûr la corde non-tendue. On fera remarquer aussi qu'une droite "tracée" et que des objets alignés relèvent de la même idée car ils émanent tous deux de l'utilisation d'une classe d'objets nommée "règle". Ces deux premiers concepts, et plus encore les outils qui s'y rapportent, permettent l'introduction de tous les polygones quelconques. Ce sont les cas particuliers qui vont nous amener à recourir à d'autres concepts.
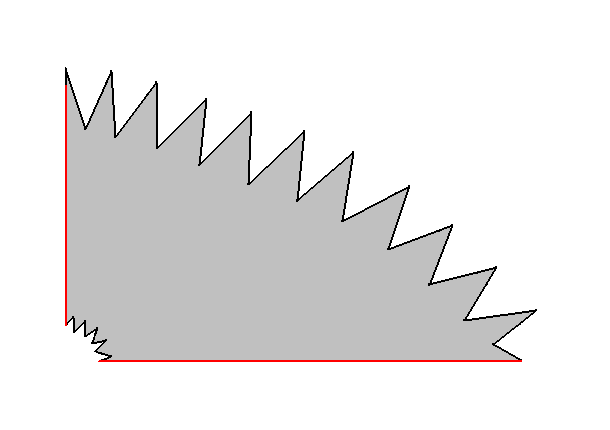
Après avoir introduit la droite par un pliage, on propose aux élèves de plier une deuxième fois leur règle. Chacun s'exécute. On obtient alors des secteurs angulaires (faire remarquer qu'il ne s'agit jamais que d'une deuxième droite). On observe que certains sont plus ouverts que d'autres, ou que certains pourraient presque se superposer, donc pourraient être considérés comme identiques. Maintenant que l'on a plié une règle au hasard, ne pourrait-on pas trouver une manière de plier qui soit différente des autres, qui ait une particularité supplémentaire ? On laisse les élèves chercher jusqu'à ce que quelqu'un propose de replier la première droite exactement sur elle-même. On obtient alors un gabarit de secteur angulaire particulier que l'on nomme "équerre", mais l'élève de CE1 est encore incapable de voir une quelconque particularité dans ce "coin". C'est à l'enseignant de faire remarquer qu'il relève de la même "forme" que les coins du tableau. Il déchire alors le coin de son équerre et demande aux élèves si cette dernière permet toujours d'opérer les mêmes vérifications. On constate que oui. On déchire alors le coin des équerres fabriquées par les enfants et on leur demande de chercher dans la classe, à l'aide de leur équerre fabriquée, d'autres occurrences de ce secteur angulaire apparemment particulier. Les exemples ne devraient pas manquer : portes, fenêtres, tables, livres, cahiers, lattes du plancher, bancs, murs (parfois), vitres, étagères, affiches murales, etc. Pris à ce stade, la grande majorité des élèves considèrent qu'un bureau dont les coins sont arrondis par sécurité a lui aussi des angles droits, indépendamment de l'aspect du coin. On veillera à ce que cela deviennent une évidence admise pour tous, ne serait-ce que par connivence, pour éviter la confusion aux effets désastreux : l'angle, c'est le coin. L'angle est une classe d'équivalence de secteurs angulaires superposables qui découle en réalité de la direction relative de deux droites. La proximité de leur point d'intersection n'est pour ainsi dire pas un endroit particulier et on doit veiller à ce qu'elle ne monopolise pas l'attention de l'enfant. On pourra aussi faire constater qu'un rectangle tracé au tableau par l'enseignant possède 4 angles droits, tout comme les tables. De là, on comprend que c'est l'équerre qui va nous permettre de tracer un rectangle convenable. L'équerre fabriquée par les élèves est conservée pour faire des vérification mais l'enseignant va fabriquer dans des feuilles A3 de nouvelles équerres "anti-mauvaises habitudes". Pour cela, il va reprendre la procédure des élèves, mais aussi repasser au marqueur les segments utiles, scotcher l'équerre pour éviter que l'élève ne joue trop avec, et découper en pointes toutes des zones inutiles. Voici un schéma d'équerre améliorée :

La première étape est de laisser l'élève découvrir l'équerre "améliorée" et la manière de tracer un angle droit avec. Ensuite, on propose aux élèves de répéter l'opération en réutilisant les droites déjà tracées. Le rectangle s'obtient par "répétition des angles droits". On peut ensuite expérimenter d'autres supports comme le tableau. L'utilisation des règles et équerres du commerce est évidemment exclue. On utilise uniquement les règles et les équerres fabriquées dans du papier déchiré.
On utilise pour cela une équerre de maçon qui est une grande boucle de corde fermée et divisée en 12 parties égales. On l'utilise en formant un triangle 3,4,5 qui a obligatoirement un angle droit. On utilise également une corde tendue pour tracer les segments. Il faut éviter de faire trop de groupes, l'autonomie pour la géométrie au sol semble être assez longue à venir.
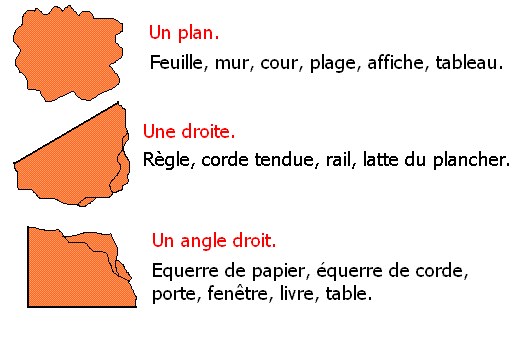
Inutile de faire une belle trace dans un cahier que les élèves n'ouvriront jamais au moment où ils en auront besoin. Il vaut mieux faire une affiche qu'ils peuvent regarder de manière rapide et non contraignante. On y collera des miniatures de plans, règles et équerres faites dans du papier de couleur. On utilisera des couleurs différentes pour séparer l'objet conceptuel des occurrences matérielle considérée comme relevant de ce concept. Exemple d'affiche :
Une fois que l'on sait tracer un rectangle, on peut s'intéresser au cas du carré. Dans un premier temps, il faut que les élèves mettent des mots sur la façon dont ils différencient un carré d'un rectangle. C'est seulement une fois que l'on est arrivé à la conclusion qu'un carré a 4 côtés de même longueur que l'on peut faire chercher aux élèves quels outils on peut prendre pour se repérer et conserver la même longueur. Parmi toutes les possibilités, on gardera la corde. Dans un premier temps, c'est l'enseignant qui montre au tableau comment tracer un carré, en montrant bien que l'on refait tout ce qui a été fait pour le rectangle, mais avec une particularité en plus. On peut aussi inviter des élèves à faire les mêmes gestes au tableau, mais pas sur feuille. Dans un deuxième temps, on peut tracer un carré dans la cour pour voir les techniques à des échelles différentes et réutiliser des outils différents comme l'équerre de maçon.
On peut essayer de faire tracer un carré sur feuille mais l'utilisation de la ficelle est très délicate sur papier et à petite échelle. L'idéal est de "bloquer" une distance en faisant 2 noeuds dans la ficelle. Cette distance déterminera la longueur des côtés du carré. Ensuite, il faut que les élèves se mettent un peu de feutre sur l'épaisseur de l'ongle (du doigt mobile) et qu'ils fassent leurs repères sur les côtés du carré avec l'ongle. En effet, le crayon introduit une inclinaison de la ficelle par rapport à la feuille qui perturbe fortement le travail sans que les élèves ne puissent comprendre facilement pourquoi. Bien sûr, cela pose le problème des élèves qui ont l'ongle coupé trop court ou qui le ronge.
En utilisant la corde pour reporter ou (conserver) des distances on peut tracer :

Olivier Batteux