Retour aux ressources pédagogiques
* Dans l'énoncé d'un problème, un mot-clé n'est jamais suffisant pour choisir une opération. Par exemple, le terme "plus que" n'entraîne pas forcément une addition, bien qu'il soit porteur d'une information clé. Nous verrons un peu plus loin la place des mots importants dans la résolution de problèmes.
* Le dessin (et à fortiori tout schéma abstrayant la matérialité sensible de l'histoire) est une procédure peu efficace chez l'enfant pour choisir la bonne opération. Les adultes pensent souvent le contraire car eux sont capables de produire des dessins efficaces. Mais l'adulte ne se rend généralement plus compte que son dessin est influencé par des constructions abstraites qui découlent des représentations des opérations qu'il a construites. Autrement dit, chez l'adulte, c'est l'opération qui permet de trouver le dessin et non l'inverse. Le dessin de l'enfant n'est pas influencé par ces constructions abstraites. C'est un dessin naïf et l'enfant peut difficilement s'en servir comme d'une procédure de résolution.
Dans un problème, les nombres sont soit liés entre eux par un champ (additif ou multiplicatif), soit dépourvus de lien. Il n'existe que 2 champs différents :
Le plus souvent, un mot clé permet d'identifier le champ qui relie 2 nombres. Voici un exemple de problème "Un camion transporte 300 boîtes contenant chacune 6 oeufs. Lors d'une secousse, 15 boîtes tombent du camion." Dans ce problème :
On remarque que si une analyse complète des relations est possible, elle n'est pas forcément nécessaire pour résoudre le problème. Si la question était "Combien d'oeufs y avait-il dans le camion avant la secousse ?", il n'aurait pas été nécessaire d'utiliser toutes les données et l'analyse d'un seul des 3 champs présents suffisait.
Il arrive fréquemment qu'un problème porte dans ses mots clés la trace d'un champ liant une donnée du problème avec un nombre qui ne figure pas explicitement dans le problème. Cela peut être très perturbant pour les élèves qui cherchent des solutions simples pour contourner leurs difficultés de compréhension en lecture. Exemple : "Aujourd'hui, l'épicière a vendu 4 boîtes de 6 oeufs. Combien d'oeufs a-t-elle vendus aujourd'hui ?" Dans ce problème, le verbe "a vendu" met en évidence le champ additif liant le nombre de boîtes vendues mentionné dans le problème avec le nombre de boîtes en stock qui n'est pas donné dans le problème. Le mot clé "de", qui met en évidence le champ multiplicatif liant 4 et 6, est beaucoup plus discret alors que c'est lui qui aide réellement à résoudre le problème. Il faut donc comprendre que les champs relient des nombres entre eux et qu'il est indispensable d'identifier les nombres liés par un champ. Identifier un champ par un mot clé n'est pas suffisant, même s'il n'y a que 2 nombres qui apparaissent dans le problème, nous venons de le voir dans cet exemple.
Au sein du champ additif, on ne peut pas choisir entre addition et soustraction en se servant des mots clés. Pour cela, il faut explorer le champ additif suivant 3 approches différentes et complémentaires :
* La question du point de vue : Dans l'histoire "Jean donne 3 bonbons à Léa", l'opération dépend du point de vue que je choisis de me donner. Ce sera une soustraction si je me place du côté de Jean, mais une addition si je me place du côté de Léa. On remarquera aussi que, simplement dans la langue, les termes "plus que" et "moins que" peuvent s'échanger mutuellement avec un simple changement de point de vue. Lorsqu'une question est imposée à la fin du problème, c'est elle qui impose au lecteur de considérer l'histoire selon un certain point de vue.
* La question de l'unité (nombre de...) et du langage : Une addition est toujours une réunion de deux ensembles. Elle n'est possible que si je dispose d'un mot pour parler de la nature de l'ensemble final. Il peut s'agir du mot utilisé pour les 2 nombres additionnés (3 choux plus 5 choux égal 8 choux), ou bien d'un hyperonyme (3 choux plus 5 carottes égal 8 légumes). Paradoxalement, l'enfant ne commence à comprendre ce qu'est une addition qu'à partir du moment où il se montre capable de s'abstenir de la faire.
* La question de la disjonction, de l'inclusion intégrale et de la partie commune : S'il y a dans ce chapitre une approche encore plus capitale que les 2 autres, c'est à l'évidence celle-ci.
a) Additionner, c'est s'autoriser à réunir au moins 2 ensembles totalement disjoints, c'est à dire sans aucune partie commune. S'il y a intersection, partielle ou totale, entre les 2 ensembles, alors l'addition est impossible car elle revient à compter deux fois certains éléments et pas d'autres, et le nombre qui en résulterait serait un non-sens par rapport à l'histoire. Pour les matheux (pardon aux autres), 2 ensembles présentant une intersection peuvent être additionnés mais la somme des cardinaux n'est pas égale à la réunion, la différence entre les deux étant le cardinal de l'intersection. Voici un schéma avec des exemples :
b) Soustraire c'est (entre autre) extraire d'une collection tout ou partie des éléments qui la composent. Pour soustraire 5 carottes, je dois d'abord disposer d'une collection d'au moins 5 carottes, sans quoi il est rigoureusement impossible de procéder à l'extraction. Mais il faut surtout que dans le sens que je donne au problème, j'admette que les 5 carottes faisaient préalablement déjà partie de l'ensemble dont je souhaite les extraire. Par exemple, dans des histoires comme "Maman a 8 carottes. Elle en mange 5." ou "Mamie a 8 carottes. Elle en arrache 5 autres dans son jardin", la question à se poser est : "Les 5 carottes faisaient-elles partie des 8 carottes précédentes, ou s'agit-il de 5 autres carottes ?". C'est seulement parce que les 5 carottes faisaient toutes partie des 8 du début de l'histoire que l'on peut faire une soustraction. Avec un schéma :
Il y a 3 manières chez l'enfant de concevoir la soustraction. Elles doivent être abordées en même temps et non les unes derrière les autres. Ce n'est que plus tard que l'enfant pourra suffisamment abstraire ces approches pour comprendre qu'elles sont équivalentes. Voici un schéma représentant ces 3 approches et des pistes pour construire leur équivalence.
Il est important pour l'adulte de distinguer 2 situations totalement différentes pour l'enfant qui commence l'apprentissage des choix opératoires. En effet, plus l'enfant est proche du début de l'apprentissage, plus une opération veut dire une histoire. Or selon les problèmes, le sens que l'on donne à ce présupposé peut varier du tout au tout.
Cas "direct" : Prenons l'histoire "Manon a 5 bonbons. Son frère lui en donne 3 autres. Combien Manon a-t-elle de bonbons ? On attend alors de l'élève qu'il admette que cette histoire peut se représenter par l'écriture "5+3". Cela ne pose pas de réel obstacle car :
Dans un tel cas, un "fait de rassemblement" raconté dans l'histoire est symbolisé par l'écriture d'une opération qui veut dire rassembler. C'est ce que nous appellerons les "cas directs", ces cas étant naturellement ceux qui posent le moins de problèmes aux enfants. Dans la pratique, quand on demande à des enfants d'inventer des problèmes illustrant une opération particulière, ils ne proposent spontanément que des cas directs.
Cas "indirect" : Prenons l'histoire " En course, Maman a dépensé 16 euros. Il lui reste encore 8 euros. Combien d'argent Maman avait-elle avant d'aller en course ?". On attend de l'élève qu'il fasse correspondre à ce problème l'opération notée 16+8. Pourtant, pour l'enfant débutant, 16+8 veut dire "rassembler 16 euros et 8 euros". Or dans le déroulement de l'histoire, il n'y a pas de "fait de rassemblement" entre 16 euros et 8 euros. Ces euros, qui au contraire se séparent, ne se reverront plus (à moins que Maman ne dévalise le magasin pour récupérer son argent, mais c'est une autre histoire !). On admet (et requiert) pourtant l'écriture 16+8 car il suffit pour qu'elle soit recevable que le lecteur puisse lui donner un sens, pas nécessairement qu'elle reproduise la matérialité de l'histoire. Ici, il peut s'autoriser à rassembler les 16 euros et les 8 euros car il peut donner à la réunion des euros restant et des euros dépensés le sens "d'euros possédés avant la dépense". L'écriture de cette addition est donc recevable dans cette histoire, bien qu'elle ne contienne aucun "fait de rassemblement".
Les cas qui posent le plus de problèmes aux enfants sont évidemment les cas indirects. Pour lever ce problème, il convient d'abord lors de l'introduction des opérations par des cas directs de laisser la porte grande ouverte sur les cas indirects, donc de ne pas prétendre à une définition exhaustive du problème-addition devant des CP ; ensuite de travailler sur les notions d'inclusion/disjonction dans le champ additif et de faire débattre les enfants autour d'objets comme ceux que nous proposons Vincent Cordebard et moi-même sous le titre de "correspondance texte littéraire / texte mathématique". Proposer aux enfants de résoudre des problèmes "indirects" avec du matériel (manipulation de type GS) avant d'introduire les écritures peut être également un bon parachute pour la suite.
En maternelle, c'est comme d'habitude la dimension langagière qui est privilégiée. On veillera dés le plus jeune âge à parler de "nombre de..." et non de nombre à vide, comme le conseille Stella Baruk. Dans les classes doubles MS/GS, on peut par exemple, lors des rituels, demander à des MS de compter les petits garçons, puis les petites filles, puis demander à un GS de compter les enfants (vu récemment dans la classe d'une collègue). L'enseignant inscrit ensuite au tableau par exemple : 12 filles ; 13 garçons ; 25 enfants. Il faut également que l'adulte donne tout de suite le bon exemple quant à l'usage des termes nombre, numéro et chiffre, et qu'il reprenne l'enfant quand c'est nécessaire. En fin de grande section, un élève peut faire la différence entre ces 3 notions s'il a bénéficié du bon exemple de la part des adultes et d'un apprentissage du nombre non conditionnant (voir le logiciel "Je compte, ça compte").
Cette approche langagière va nous amener à vivre des problèmes dès la grande section. L'enseignant raconte une histoire simple et les élèves la miment avec de vrais objets (bonbons, figurines...). Ils peuvent soit compléter l'histoire en calculant ce qu'ils souhaitent, soit répondre à une question imposée par l'enseignant. Il convient de faire les deux de façon alternative. Ce type de situation va nous ouvrir une porte vers la construction de l'abstraction du nombre. En effet, après avoir résolu un problème de fourchettes en jouant avec de vraies fourchettes, on peut demander aux enfants si on aurait pu trouver le même résultat sans fourchettes, en utilisant des jetons à la place. Pour les élèves, ça n'a rien d'évident. Il faut alors reprendre la même histoire avec des jetons à la place des fourchettes et faire constater aux élèves que l'on trouve le même nombre de jetons que de fourchettes dans la simulation précédente. On peut aussi jouer sur la couleur des jetons : pour représenter des tomates, faut-il forcément prendre des jetons rouges ? D'autre part, après avoir conclu un problème en comptant (par exemple de gauche à droite) les objets finals, on peut demander aux enfants si on aurait trouvé le même nombre en comptant dans l'autre sens (par exemple de droite à gauche). Comme plus de la moitié des enfants de grande section répondent "non" (Vous n'y croyez pas ? Essayez !), on recompte dans l'autre sens et on constate que ça ne change pas le résultat du problème. On peut aussi répéter l'expérience en changeant l'ordre des objets. C'est au travers de ce genre de petites situations, qui peuvent parfois être ajoutées aux rituels et donc étalées sur l'année, que l'élève de grande section consolide sa compréhension du nombre.
Toujours dans le cadre de ce travail sur la compréhension de la langue, on peut travailler dès la maternelle la question de l'autre et de l'inclus. Cela permettra aux enfants le jour venu de choisir entre addition et soustraction, même si on ne formalise pas les choses de cette façon en maternelle. Par exemple, l'enseignant raconte l'histoire : "Tom a 5 billes dans sa poche. Il perd 3 billes car sa poche a un trou." et demande aux enfants : "Les 3 billes perdues font-elles partie des 5 billes du début, ou est-ce que c'est 3 nouvelles billes ?". Et c'est tout, pas besoin d'aller plus loin pour l'instant.
En fin de maternelle, l'enfant doit être capable de comprendre et d'employer les termes "nombre de...", "plus de... que de...", "moins de... que de...", "autant de... que de...". Si la classe est à l'aise dans ce domaine, on peut faire une explicitation sur la polysémie du mot "plus" en français. En effet, le mot "plus" utilisé dans l'expression "plus de... que de..." n'a pas le même sens que le "+" de l'addition. L'un renvoie à une réunion de 2 ensembles, l'autre à leur différence. On pourra faire remarquer aux enfants que s'ils se prononcent pareil, l'un se note "plus" en lettres alors que l'autre se note par un signe (+). Si on fait ce travail, le signe + sera utilisé au tableau par l'enseignant mais pas par les enfants. On laissera sa "vraie" introduction à la classe de CP. En tout état de cause, les termes d'addition et de soustraction ne sont pas à utiliser en maternelle. Le rôle de la maternelle n'est pas de formaliser mais d'autoriser l'abstraction qui ne sera formalisée que plus tard.
Outils relatifs à cette partie : Le logiciel "Je compte, ça compte" et le Jeu du comptage argumenté.
Le CP est la classe où l'élève apprend à formaliser par un nom et une écriture les opérations que l'école maternelle lui a appris à penser. Le concept d'addition doit être construit avant que le signe + ne soit introduit, mais cela ne veut pas dire forcément que ce signe arrive le plus tard possible : le travail fait en maternelle est aussi à prendre en compte.
Pour introduire le signe + en CP, il faut soi-même avoir en tête deux repères fondamentaux : d'une part, avoir compris qu'une opération n'est pas son écriture (5+3 étant le résultat d'une addition), et d'autre part, avoir en tête l'adage d'Alain Connes "La seule autorité quand on fait des mathématiques, c'est soi-même.". Expliquer l'addition pour la première fois à des CP peut (et devrait) se faire de façon très scientifique, mais en s'appuyant d'abord sur des exemples. On peut partir d'une histoire comme "Il y a 5 enfants dans la classe de CP. Ensuite, 7 CE1 viennent s'installer à côté d'eux". La question à poser aux enfants est "Dans cette histoire, est-ce que je peux m'autoriser à rassembler les CP et les CE1 ?". Les enfants comprennent ce genre de question sans problème et répondent oui. Pour vérifier que l'on peut vraiment les rassembler, il faut se demander ce que l'on obtient si on s'autorise ce rassemblement. Il faut bien faire remarquer aux élèves que cette réunion ne donnera ni des CP, ni des CE1, mais des élèves tout court, ou des enfants. Ceci fait, on peut donc confirmer aux élèves qu'ils avaient raison de s'autoriser, par rapport à cette histoire, à rassembler les CP et les CE1. On définit alors l'addition pour les élèves comme étant ce qui se passe dans leur tête au moment où ils s'autorisent à faire ce rassemblement. Se pose alors le problème de garder une trace du résultat de ce rassemblement (Combien d'élèves obtient-on ?). Les élèves vont proposer 12 élèves, ce qui est une bonne réponse, mais on peut leur faire remarquer que si on écrit le résultat de cette façon, ça va nous aider à nous souvenir du résultat final, mais ça ne va pas nous aider à nous souvenir de l'histoire. Pour cela, il faut utiliser une autre écriture du résultat de l'addition, à savoir 5+7 élèves, en faisant bien remarquer que "5+7" est une écriture du nombre 12. C'est ainsi qu'apparaît le signe +. On pourra parler d'écriture "historiée" car d'une part elle nous permet de nous souvenir de l'histoire, et d'autre part elle ouvre une porte vers la création d'autres histoires aboutissant elles aussi au nombre 12. Ensuite (dés cette même séance), on proposera d'autres histoires et les élèves devront dire s'ils peuvent s'autoriser ou pas à rassembler les nombres mis en jeu. La question n'est pas de savoir si on a le droit mais de savoir si ça a un sens. Impérativement, seuls les rassemblements pour lesquels on peut donner un nom à ce que l'on obtient pourront être acceptés. Une fois un rassemblement accepté on écrit son résultat de 2 façons différentes : d'une façon condensée, par exemple "5 bonbons" ; et d'une façon historiée, par exemple "3+2 bonbons". Cette démarche est à conserver pendant toute la scolarité : l'élève ne doit jamais pouvoir se dire "je fais une soustraction car aujourd'hui c'est le jour des problèmes où qui faut faire des soustractions". Il doit toujours être confronté à plusieurs possibilités et ainsi être obligé de faire des choix. En CP, alors que l'élève ne connaît que l'addition, il est impératif de lui proposer de façon mélangée des situations relevant de l'addition et des situations où on ne peut pas faire d'addition, sans quoi il n'apprendra pas à différencier ces situations. Il faut aussi proposer des histoires avec plus de 2 données numériques pour que se pose la question indispensable : "Additionner quoi avec quoi pour obtenir quoi ?".
Il faudra avoir en tête ces mêmes repères pour introduire la soustraction. Son sens premier sera de préférence celui de "enlever" mais il faut veiller dès le départ à ce que cette conceptualisation ne soit pas fermée. La soustraction sera ce qui se passe dans sa tête au moment ou on s'autorise à enlever d'une collection une partie de cette collection, la mémoire de cette soustraction et de son histoire pourra être gardée en écrivant son résultat sous la forme 5 - 3 (par exemple). Dans un premier temps, on va proposer des histoires et ce sera aux élèves de dire si on peut faire correspondre à cette histoire une écriture additive, soustractive, ou rien de cela. Mais on ne propose pas à ce stade d'histoires relevant d'autres conceptualisations de la soustraction.
Dans un deuxième temps (qui doit arriver très vite !), on fera découvrir aux élèves que leur manière de penser la soustraction n'est pas encore complète en leur proposant des problèmes que l'on peut résoudre par la soustraction, mais qui ne relèvent pas de l'idée d'enlever. Supposons qu'il y ait réellement dans la classe Léa, 6 ans, et Tom, 8 ans et que les élèves connaissent déjà ces camarades et leur âge. L'enseignant pose comme problème : "Léa a 6 ans et Tom 8 ans. Combien d'années Tom a t-il de plus que Léa ?". On demande aux élèves de dire la réponse sans calculer. Ils devraient trouver 2 ans sans trop d'aide. Ensuite, il faut s'appuyer sur les compétences en matière de calcul. Connaissait-on une opération qui à 8 et 6 associe 2. Les élèves vont trouver 8-6. On émet alors l'hypothèse qu'on peut résoudre ce type de problème avec une soustraction. On valide ensuite cette hypothèse en mimant des histoires du même type, dans lesquelles on ne remplace que les nombres et les mots "ans / années" par un objet disponible. On conclut que ce type d'histoires relève aussi de la soustraction, même si on n'a pas l'impression d'enlever.
On peut répéter un tel temps de classe avec une histoire du type : "Pierre a 4 billes. Il voudrait en avoir 7. Combien lui en manque t-il ?". Comme dans l'exemple précédent, on trouve d'abord la réponse à la question par le mime et on s'appuie sur les connaissances en calcul pour trouver l'opération qui pouvait correspondre et qu'on a fait sans le savoir. On émet l'hypothèse que ce type de problème relève également de la soustraction et on la valide par des histoires dont on change les nombres et objets, mais pas la structure de l'histoire. L'objectif n'est pas de formaliser toutes les approches possibles de la soustraction, ce sera fait en CE, mais de sensibiliser à la multiplicité des utilisations de la soustraction, et à maintenir en état de "chantier conscient" la construction de son sens. On notera au passage que ces substitutions (nombres et objets sans toucher la "structure") aident l'enfant à saisir l'abstraction par laquelle on considère comme relevant de la même idée (l'opération) des histoires qui parlent de choses différentes.
En complément, on peut demander aux enfants comment ils avaient fait pour trouver 2 ans dans leur tête pour l'histoire "Léa a 6 ans et Tom 8 ans. Combien d'années Tom a t-il de plus que Léa ?" alors qu'ils ne savaient pas encore qu'on pouvait faire une soustraction. Certains élèves vont dire ou montrer, d'une façon ou d'une autre qu'ils ont complété, surcompté, etc... On fera alors remarquer que cela a bien fonctionné, donc que c'est aussi une façon de calculer les soustractions d'une autre manière. Cela permet d'introduire une procédure de calcul en rapport avec le sens d'histoires. Ceci fait, on pourra faire constater aux élèves que ces différentes méthodes permettent de calculer toutes les soustractions, quelles que soient les histoires dont elles proviennent. Par exemple, dès lors que l'écriture 15 - 13 est possible, alors on peut la calculer par complément, même si elle provient d'une histoire où la soustraction avait le sens d'enlever.
Pour finir, il ne faut pas oublier que l'année de CP est aussi une année où l'on donne des situations problèmes sur la numération décimale et des problèmes ouverts multiplicatifs ou de partage qui permettront à l'élève d'avoir, le jour où ce sera devenu nécessaire, le vécu l'autorisant à penser la multiplication et la division. Ces situations sont d'excellentes occasions de réinvestir et consolider ce qui a été appris sur l'addition, notamment au travers de procédures faisant intervenir l'addition itérée comme procédure semi-experte (problème relevant de la multiplication) ou de tâtonnement (problème de partage). Pour autant, cela ne doit rien changer au fait que dans ces situations l'élève est laissé libre de sa procédure (dessin, manipulation).
Le CE1, première partie : La première partie du CE1 est basée sur la consolidation des repères dans le champ additif et donc la capacité à choisir entre addition, ou soustraction, ou pas d'opération connue possible. Cela passe notamment par l'installation de la triple représentation de la soustraction, d'abord perçue comme le simple fait d'enlever, et par le travail sur la notion d'inclusion/disjonction expliquée dans la partie théorique (voir les 4 et 5 de la partie théorique). Contrairement aux dessins abstraits, poser oralement la question de ce qui "fait partie de" et de ce qui "est autre chose" peut servir de procédure de résolution dans le champ additif, à condition de se donner un peu de temps d'entraînement pour installer cette "gymnastique" de raisonnement.
Cette approche est à mettre en relation avec le travail sur les problèmes "indirects" qui posent encore problème aux enfants et que l'on va donc travailler beaucoup plus intensément qu'en CP (voir le 6 de la partie théorique). C'est le moment d'insister une nouvelle fois sur le caractère trompeur des mots (ex : "perd" qui peut entraîner aussi une addition) et de verbaliser (et faire verbaliser) dans un langage accessible aux enfants les différences entre problèmes directs et indirects expliquées au niveau adulte dans le 6 de la partie théorique ("ça se rassemble dans l'histoire" ou "c'est moi qui rassemble dans ma tête parce que je peux dire ce que ça représente").
On peut également expliquer aux enfants (si on les sent prêts ou presque) pourquoi on utilise l'astuce de l'inclusion/disjonction dans le champ additif : cela évite de mettre en place un grand foutoir avec des opérations prioritaires pour chaque mot et des inversions d'opération quand le déroulement du temps considéré change. En français, le mot "perd" renverrait à une soustraction quand on considère l'histoire dans le sens de son déroulement (ex : Pierre a 5 billes. Il en perd 3. Combien restent ?) et à une addition quand on "remonte le temps". (ex : Pierre a perdu 3 billes. Il lui en reste 2. Combien en avait-il ?). On peut montrer aux enfants cette histoire de temps et de changement d'opération avec des exemples très concrets et leur expliquer que l'on utilise l'astuce de "font partie des..." ou "sont des autres..." pour éviter de se lancer sur ce terrain glissant et qui ne traite pas pour autant du cas de mots comme "donne".
La triple représentation de la soustraction peut donner lieu à la création avec les élèves d'une affiche de même type que celle proposée dans la partie théorique mais davantage adaptée aux enfants, liée à la vie de la classe et aux histoires qu'on s'y est racontées. Il ne faut pas oublier lors de cette première partie d'année que la seconde sera marquée par l'officialisation de la multiplication et qu'à ce titre il est plus que jamais fondamental de donner aussi aux enfants des problèmes ouverts, multiplicatifs ou de partage, qu'ils sont libres de résoudre par dessin, manipulation, ou addition itérée. Il est temps aussi de commencer à les mélanger avec des problèmes du champ additif pour que l'élève soit amené à se poser lui-même la question de savoir si un problème relève de procédures expertes qu'il connaît déjà ou s'il n'a pour l'instant pas d'autres choix que d'improviser une procédure personnelle de résolution.
Le CE1, deuxième partie : Cette deuxième partie d'année, plus ou moins tardive selon le niveau de la classe, sera donc marquée par l'introduction officielle de la multiplication sur la base des situations multiplicatives ouvertes et des manipulations proposées en CP et en début de CE1, voire parfois depuis la maternelle. Cette introduction (il faut considérer les cas où certains élèves n'ont pas connu les phases de préparation nécessaires) ne saurait se baser uniquement sur une schématisation abstraite conduite par l'adulte, et encore moins sur des lignes d'écriture du type 6+6+6+6+6+6+6+6+6. En effet, sa longueur produit chez l'enfant un effet de "saturation de code" qui lui fait perdre toute la signification de l'écriture, quand bien même il en comprend chacune des briques. Ce sera pour l'enfant uniquement une écriture qui se répèteras, et non sa signification, indispensable pour penser la multiplication à partir de cette voie. De même, il existe des problèmes pour lesquels l'adulte, inconsciemment, ne fait une multiplication que pour ne pas écrire une telle grande addition. C'est le cas par exemple d'un problème où on demanderait le prix de 12 tickets d'entrée à 7 euros, pire en les schématisant en croyant aider, ce qui n'a pas du tout le même sens que 12 boîtes de 7 objets. Un tel problème ne peut en aucun cas être premier dans la formalisation de la multiplication. Ce sont au contraire des éléments de langage qui dans un second temps permettront de construire l'équivalence entre les deux exemples précédents.
L'introduction formelle de la multiplication part au contraire de situations fortement concrètes (objets, boîtes, paquets, rangées) vers les très diverses formulations qui existent dans la langue pour parler de ces situations et actions, puis vers le relevé dans ces formulations des mots clés déterminants qui me permettront ensuite de différencier le champ additif du champ multiplicatif. Il faut que l'enseignant soit vigilant dans cette phase : ne pas relever abusivement de mots pouvant conduire aussi dans certains cas au champ additif, ne pas non plus se limiter à un panel trop appauvri de la diversité des verbalisations recherchée juste avant. Ce sont ces éléments de langage qui seront constitutifs de la réussite en résolution de problèmes, à condition toutefois de s'appuyer dessus avec intelligence : la globalité des histoires doit garder un sens même si on exploite particulièrement certains mots révélateurs, sinon on est assuré du désastre, ne serait-ce que par les effets de champs perturbateurs mentionnés dans la partie théorique. Il est donc important d'envisager l'installation des compétences associées également en termes de fonctionnement d'ensemble, donc d'utiliser immédiatement les premiers relevés pour faciliter le choix entre "famille addition-soustraction" ou famille "multiplication-division" dans des histoires, et d'aborder le plus grand nombre d'histoires possible avec la plus grande variété possible.
Il sera important ici d'utiliser comme "pièges" quelques problèmes relevant de la division, pour installer en tant que telle dans la tête des enfants la problématique, qui se posera bientôt, du choix entre multiplication et division dans le champ multiplicatif. Ils ne doivent pas apprendre à choisir de façon automatique la multiplication dès qu'ils voient un signe du champ multiplicatif. Il n'y aura pas ici de très gros obstacle à franchir car la notion d'ordre grandeur permettra de "tricher" efficacement pour contourner le problème.
Comme pour l'addition et la soustraction, l'écriture du résultat ( exemple 3x5 ) de la multiplication marque la rupture entre la résolution du problème et le calcul. Passé ce cap, comme ce que j'ai écrit est déjà une écriture du résultat, ce qui suit n'est plus qu'un changement d'écriture (appelé calcul) dans lequel je peux utiliser toutes les règles connues sur les transformations d'écriture, sans me soucier de l'histoire d'origine. C'est le même phénomène que pour la soustraction précédemment, quand on calculait un reste en complétant ou un complément en enlevant. L'apprentissage clé ici sera de se faciliter la vie en utilisant la commutativité, même si ensuite la distributivité aura elle aussi un rapport avec cette étape logique. Comme elle se situe avant tout dans le registre de la règle de transformation des écritures, l'essentiel de l'apprentissage de la commutativité avec les enfants réside tout simplement dans le fait de constater de toutes les façons possibles que ça fonctionne. Cela n'empêche pas pour autant de compléter rapidement par des justifications théoriques visibles, par exemple d'aligner des objets en lignes et en colonnes, et de constater qu'en changeant simplement de point de vue autour d'une table ou de façon d'entourer, je décris la même réalité de deux façons différentes.
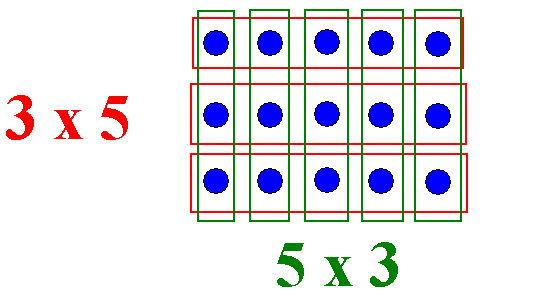
La trace de ce travail sera la constitution d'un tableau des mots repères avec (seulement) deux colonnes, le fait qu'elles ne soient que deux étant déjà en soi un apprentissage par rapport aux méthodes implicites ou à structure contre-productive.

La constitution de notions de référence n'est pas un excès d'abstraction si elle n'est pas première et si elle ne prend pas la place de ce qui les produit (et qui a été détaillé plus haut). Un des repères les plus important ici est la nécessité absolue de l'identité pour pouvoir considérer le champ multiplicatif.
On pourrait ajouter dans la famille addition / soustraction le mot "dont", qui renvoie souvent à la soustraction, et dont la compréhension semble être une acquisition longue et difficile pour les enfants. Elle nécessite un travail de langage spécifique, d'où à la fois la difficulté et la nécessité de considérer avec les enfants les notions d'inclusion / disjonction mentionnées dans la partie théorique.
Les deux premiers trimestres du CE 2 sont des temps de consolidation des notions détaillées dans les deux parties précédentes (CP et CE1). Cela permet à ceux qui n'ont pas connu cette démarche en cycle 2 de se mettre au clair, et aux "retardataires" de bénéficier du temps dont ils ont besoin sans se retrouver déjà dans un groupe de différenciation tel que proposé dans la partie suivante (CM). Ceux qui semblent avoir compris ne perdent pas réellement de temps à "réviser" à ce stade si les histoires sur lesquelles ils travaillent ne sont pas d'une pauvreté langagière démobilisante.
Dans cette optique, le troisième trimestre doit être un temps où on utilise ce qui a été appris précédemment dans le cadre d'histoires de plus en plus longues, riches par leurs formulations, complexes, variées, et progressivement plus éloignées du vécu des enfants.
Le CM est un stade où un travail différencié est absolument indispensable car ce qui permet d'aller plus loin à ceux qui ont parfaitement acquis les objectifs ci-dessus ne peut qu'enfoncer les autres encore plus profondément dans leurs difficultés. Il est prouvé scientifiquement depuis 25 ans que ce qui est proposé ici pour les premiers donne des résultats globalement médiocres et surtout augmente fortement l'hétérogénéité des groupes d'élèves : ceux qui savent déjà l'essentiel (détaillé ci-dessus) en tirent un bénéfice réel (c'est un nouvel outil pour structurer un savoir déjà là), mais les autres s'en éloignent davantage qu'ils s'en approchent. Ce n'est pas une voie possible pour rattraper leur retard, bien que de telles pratiques soient très tentantes pour l'adulte, d'où le fait qu'on les trouve encore dans nombre de manuels.
Quand ce qui a été détaillé pour les classes antérieures n'est pas acquis en CM, c'est cette même démarche précédente qu'il faut reprendre de façon accélérée, à partir de là où les élèves en sont réellement restés. C'est souvent dès le départ que les bonnes représentations n'ont pas été posées, mais l'âge plus avancé (et donc l'expérience) des élèves permet de faire plus facilement des bons en avant ou en arrière dans la progression. La notion de métacognition est importante ici pour l'enseignant car ce sont souvent des situations où des fausses représentations anciennes et solides sont à l'origine des difficultés que l'élève traîne depuis le départ en résolution de problèmes.
Cette partie ne concerne donc que les élèves de CM qui ont parfaitement acquis les étapes précédentes. Elle traite surtout du champ additif, mais ce n'est évidemment pas le seul à travailler en CM. Ce qu'elle propose n'est en aucun cas une procédure de résolution, que ce soit pour les élèves de ce groupe ou de l'autre, car ça découle de la résolution du problème et non l'inverse. C'est davantage en termes d'arme argumentative qu'il faut voir un tel schéma :
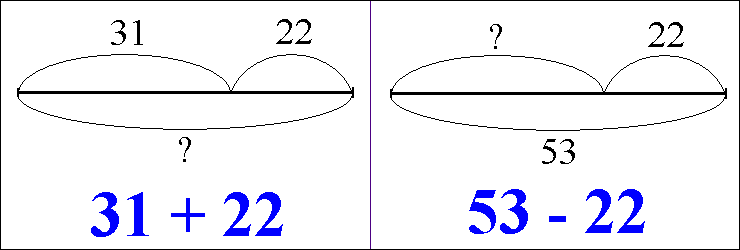
L'élève qui choisit 53-22 sait pourquoi il le fait, indépendamment du schéma qu'il propose. Mais s'il peut prouver, à partir de ce qu'il y a dans l'histoire, que seul le schéma de droite et pas celui de gauche peut la représenter, alors plus personne ne pourra lui dire que ce n'est pas une soustraction qu'il faut faire. L'établissement d'un lien histoire-schéma solide est, vis à vis d'un camarade en désaccord, une "quasi-preuve" qu'on a raison.
Une telle activité n'est possible avec un groupe d'élèves qui possède déjà les prérequis nécessaires que si les histoires proposées opposent une complexité maximale. Avec des histoires faciles, tous les élèves réussiraient individuellement à résoudre le problème, et donc de telles confrontations n'auraient aucune chance de s'établir.
Dans un autre registre, il peut être établi un lien entre les champs définis précédemment et de nouvelles notions comme l'aire, le périmètre ou la proportionnalité.
Le calendrier est purement indicatif, c'est le principe didactique qui compte. Il peut être appliqué de façon décalée ou en remédiation.
Il faut faire attention aux histoires trop faciles (et à ne pas donner une place démesurée aux "cas directs") car :
Vous pouvez envoyer vos retours à cette adresse :
![]()
Olivier Batteux